balanced search trees
Allow 1 or 2 keys per node
- 2-node: one key, two children
- 3-node: two keys, three children
Perfect balance: every path from root to null link has same length.
Symmetric order: Inorder traversal yields keys in ascending order
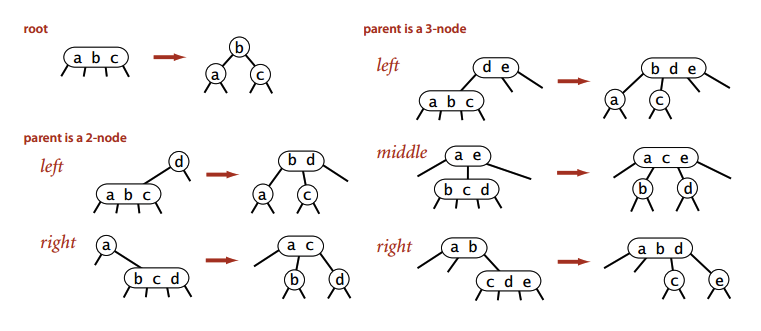
If has a temp 4-node, move the middle key above.
2-node can be converted to 3-node.
Maintains symetric order and perfect balance.
Direct implementation is complicated
red-black BSTs
Use “internal” left-leaning as “glue” for 3-nodes.
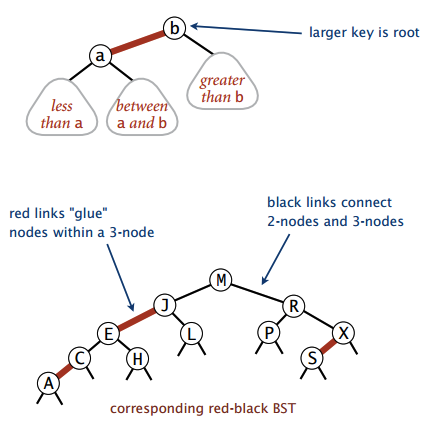
- no node has two red links connected to it
- every path from root to null link has the same number of black links
- red links lean left
Search is the same as for elementary BST (ignore color)
Most of other ops like ceiling, selection are also identical
Encode the color of links in nodes (the link pointing to their parent)
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node
{
Key key;
Value val;
Node left, right;
boolean color; // color of parent link
}
private boolean isRed(Node x)
{
if (x == null) return false;
return x.color == RED;
}
rotate left: right child red, left child black
private Node rotateLeft(Node h)
{
assert isRed(h.right);
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
return x;
}
rotate right: left child, left-left gradchild red
private Node rotateLeft(Node h)
{
assert isRed(h.right);
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
return x;
}
flip color (while one parent node has two red son links)
private void flipColors(Node h)
{
assert !isRed(h);
assert isRed(h.left);
assert isRed(h.right);
h.color = RED;
h.left.color = BLACK;
h.right.color = BLACK;
}
insertion
private Node put(Node h, Key key, Value val)
{
if (h == null) return new Node(key, val, RED);
int cmp = key.compareTo(h.key);
if (cmp < 0) h.left = put(h.left, key, val);
else if (cmp > 0) h.right = put(h.right, key, val);
else if (cmp == 0) h.val = val;
if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
if (isRed(h.left) && isRed(h.right)) flipColors(h);
return h;
}
Height of tree is in the worst case
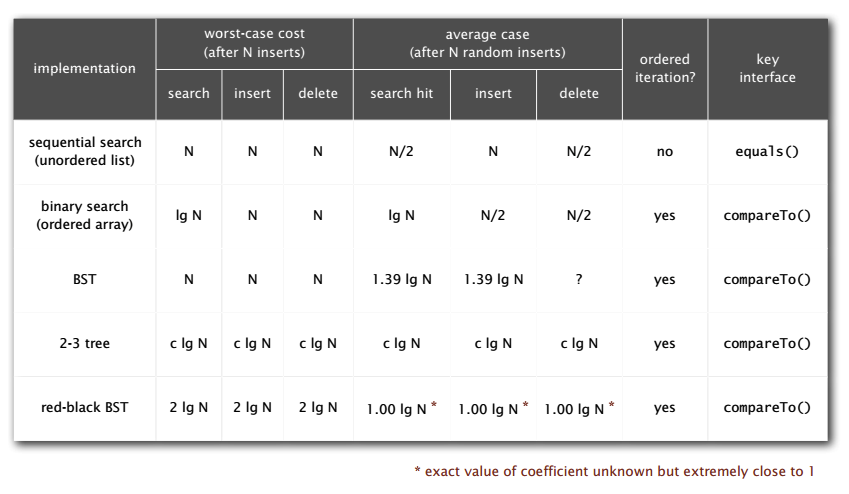
summary for symbol tables
B-trees
Generalize 2-3 trees by allowing up to M-1 key-link pairs per node.
Geometric applications of BSTs
1-d range search
extension of ordered symbol table
- insert key-value pair
- search for key k
- delete key k
- range search: find all keys between k1 and k2
- range count: number of keys between k1 and k2
Geometric interpretation
- keys are points on a line
- find and count points in given 1-d interval
line segment intersection
sweep line algorithm, horizontally.
- put x-coordinates on a PQ (or sort)
- insert y-coordinates into BST
- delete y-coordinates from BST
- range searches in BST
Kd-tree
extension of ordered symbol-table to 2d keys
- insert a 2d key
- delete a 2d key
- search for a 2d key
- range search: find all keys that lie in a 2d range
- range count: number of keys that lie in a 2d range
recursively partition plane into two halfplanes
kd-tree
works for k dimensions
interval search trees
Data are intervals.
Find all intervals in data structure that intersects a given interval.
use lo as the key
store max endpoint in subtree rooted at node
- if interval in node intersects query interval, return it
- else if left subtree is null, go right
- else if max endpoint in left subtree is less than lo, go right
- else go left
rectangle intersection
sweep line
