Hash tables

Save items in a key-indexed table (index is a function of the key).

Hash function: Method for computing array index from key.

All Java classes inherit a method hashcode(), which returns a 32-bit integer.
If x.equals(y), then x.hashCode() == y.hashCode() and vice versa.

Hash code: An int between $-2^{31}$ and $2^{31}-1$
Hash function: An int between 0 and M-1 (for user as array index)

private in hash(Key key)
{ return (key.hashCode() & 0x7fffffff) % M;} 
// get the absolute value first then remainder

Separate Chaining

Separate chaining ST using linked list

For every hash, make a linked list to store the key and value
Make $M \sim N/5$ $\rightarrow$ constant time ops.

Linear Probing

Insert: Put at table index i if free; if not try i+1, i+2, etc.

Search: Search table index i; if occupied but no match, try i+1, i+2, etc.

Array size M must be greater than number of key-value pairs N.
Works well when size of the array is significantly bigger than the number of keys.

Hash Table Context

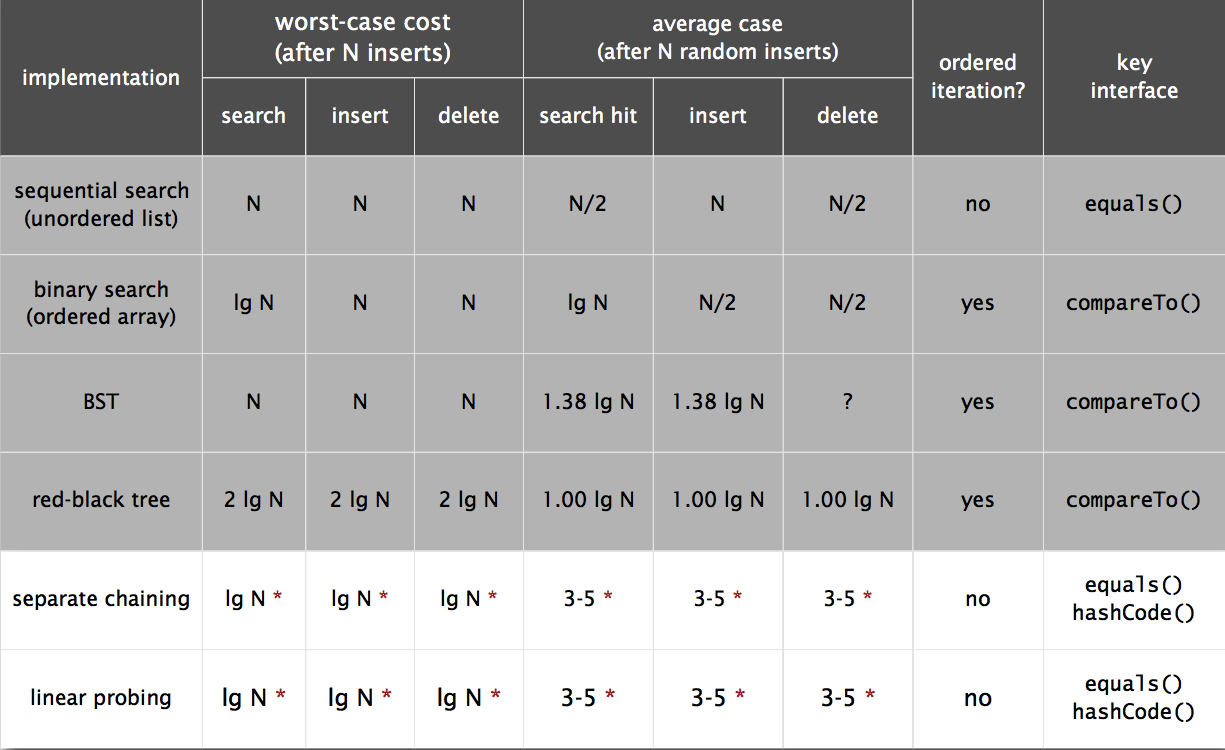
STimplement

Simple to code
Faster for simple keys
Better system support in Java for strings

java.util.HashMap
java.util.IdentityHashMap

Balanced search trees

Stronger performance guarantee
Support for ordered ST operations
Easier to implement compareTo() correctly than equals() and hashCode()

java.util.TreeMap
java.util.TreeSet

Applications

Mathematical Sets

Dictionary Clients

Indexing Clients

public class Concordance
{
   public static void main(String[] args)
   {
      In in = new In(args[0]);
      String[] words = in.readAllStrings();
      ST<String, SET<Integer>> st = new ST<String, SET<Integer>>();
      for (int i = 0; i < words.length; i++)
      {
         String s = words[i];
         if (!st.contains(s))
            st.put(s, new SET<Integer>());
         SET<Integer> set = st.get(s);
         set.add(i);
}
      while (!StdIn.isEmpty())
      {
         String query = StdIn.readString();
         SET<Integer> set = st.get(query);
         for (int k : set)
      }
  } 
}

Sparse Vectors

public class SparseVector
{
     private HashST<Integer, Double> v;
     public SparseVector()
    {  v = new HashST<Integer, Double>();  }
     public void put(int i, double x)
    {  v.put(i, x);  }
    public double get(int i)
    { if (!v.contains(i)) return 0.0;
      else return v.get(i);
    }
    public Iterable<Integer> indices()
    {  return v.keys();  }
    public double dot(double[] that)
    {
        double sum = 0.0;
        for (int i : indices())
            sum += that[i]*this.get(i);
        return sum;
    }
}

AI 2

Algorithm 17

Amazon 1

Authorization 1

Blog 3

Bootstrap 1

C++ 1

CCpp 5

CSS 2

Cloud 3

Code 1

Crawler 1

DNS 1

Database 17

DeepLearning 1

Design 16

Development 1

Docker 1

Express 1

GDB 1

Go 3

Google 4

HTML 3

IOS 1

Java 17

Javascript 4

Jekyll 1

Linux 4

MacOS 2

MachineLearning 16

Markdown 4

Mobile 1

MongoDB 2

Multi-threading 3

NAS 1

Network 11

NeuralNetwork 10

Node 1

OS 8

Public-speaking 1

Python 15

RESTful 1

Rails 9

React 1

Redis 1

Ruby 6

Shell 2

Spring 2

System 16

TCP 1

TDD 1

Thread 2

Vim 1

awk 1

git 1

jQuery 1

media 1

network 1

php 1

Princeton Algorithms P1W6 Hash Tables & Symbol Table Applications