evaluating a learning algorithm

deciding what to try next

debugging a learning algorithm

Unacceptably large errors in its predictions.

1. get more training examples - fix high variance
2. try smaller sets of features - fix high variance
3. try getting addtional features - fix high bias
4. try adding polynomial features - fix high bias
5. try decreasing $\lambda$ - fix high bias
6. try increasing $\lambda$ - fix high variance

diagnostic

A test that you can run to gain insight what is/isn’t working with a learning algorithm, and gain guidance as to how best to improve its performance.

Diagnostics can take time to implement, but doing so can be a very good use of time.

evaluating a hypothesis

training set: 70% (better randomly shuffled)
test set: 30%

training/testing procedure for linear regression

1. learning parameter $\theta$ from training data (minimizing training error $J(\theta)$)
2. compute test set error (cost function)
3. get missclassification error (percentage of wrong predictions if classification problem)

model selection and training/validation/test sets

model selection

d: what degree of polynomial to choose for hypothesis

calculate the test set error for different degrees of polynomial cnd choose the one with minimum error

evaluating hypothesis

1. training set: 60%
2. cross validation set: 20%
3. test set: 20%

Test parameters with different degree of polynomial on cross validation set. Estimate generalization error on the test set

bias vs. variance

diagnosing bias vs. variance

High bias: underfit. high training error and high validation error
High variance: overfit. low training error and much high validation error

regularization and bias/variance

regularization parameter $\lambda$

• large $\lambda$: high bias (underfit)
• small $\lambda$: high variance (overfit)

Define the cost function of training, validation and test sets without regularization terms.

1. Create a list of $\lambda$
   (i.e. $\lambda \in \{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24\}$);
2. Create a set of models with different degrees or any other variants.
3. Iterate through the $\lambda$s and for each $\lambda$ go through all the models to learn some $\theta$.
4. Learn the parameter $\theta$ for the model selected, using $J_{train}(\theta)$ with the $\lambda$ selected.
5. Compute the train error using the learned $\theta$ (computed with $\lambda$ ) on the $J_{train}(\theta)$ without regularization or $\lambda=0$.
6. Compute the cross validation error using the learned $\theta$ (computed with $\lambda$) on the $J_{CV}(\theta)$ without regularization or $\lambda=0$.
7. Select the best combo that produces the lowest error on the cross validation set.
8. Using the best combo $\theta$ and $\lambda$, apply it on $J_{test}(\theta)$ to see if it has a good generalization of the problem.

learning curve

Plot $J_{train}(\theta)$ or $J_{CV}(\theta)$ vs training set size m.
While m increases:

• increasing $J_{train}(\theta)$
• decreasing $J_{CV}(\theta)$

While bias is high:

• The final errors for both training and validation will be high and similar
• Getting more training data will not help much

While variance is high:

• large gap between final errors for training and validation sets but approach each other while m increases
• getting more training data is likely to help

neural network

• small neural network: fewer parameters; more prone to underfitting; computationally cheaper
• large neural network: use regularization to address overfitting

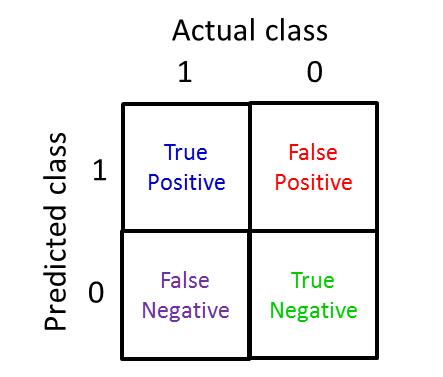
precision = (true positives)/(no. of predicted positive)
recall = (true positives)/(no. of actual positive)

use F1 score formula to evaluate algorithms: $2 \frac{PR}{P+R}$