models of neurons

Human Brain:

Stimulus $\rightarrow$ Receptors $\leftrightarrow$ Neural Net $\leftrightarrow$ Effectors $\rightarrow$ Response

• $10^{-3}$ s per operation
• $10^{10} - 10^{11}$ neurons and $6 \times 10^{13}$ connections

• $10^{-16} J$ per operation

• Synapses with associated weights : j to k denoted $w_{kj}$
• Summing function: $u_k = \sum_{j=1}^m w_{kj} x_j$
• Activation function: $y_k = \phi(u_k + b_k)$
• Bia $b_k$: $v_k = u_k + b_k$ or $v_k=\sum_{j=0}^{m} w_{kj}x_j$

activation function

1. threshold unit
2. piece-wise linear
3. sigmoid: logistic $\phi(v)=\frac{1}{1+exp(-av)}$ and $\phi'(v) = a \phi(v)(1-\phi(v))$
4. signum function
5. sign function
6. hyperbolic tangent function

stochastic models

Instead of deterministic activation, stochastic activation can be done. Activated with a probability of firing $P(v)$.

A typical choice: $P(v) = \frac{1}{1+exp(-v/T)}$. T is a pseudotemperature.

In computer simulation, use the rejection method.

definition of a neural network

• signals are passed between neurons over connection links
• each connection link has an associated weight, which typically multiplies the signal transmitted
• each neuron applies an activation function to its net input to determine its output signal

feedback

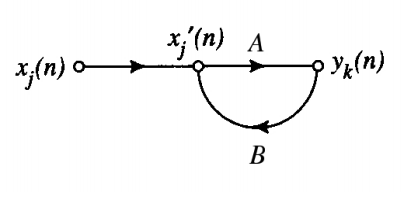
\[y_k(n) = A[x_j ‘(n)]\]

\[x_j ‘(n) = x_j(n) + B[y_k(n)]\]

So:

\[y_k(n) = \frac{A}{1-AB}[x_j(n)]\]

$\frac{A}{1-AB}$ is called the closed-loop operator and $AB$ is the open loop operator.

Substitute $w$ for $A$ and unit delay operator $z^{-1}$ for $B$.

\[\frac{A}{1-AB}=w(1-w z^{-1})^{-1}=w \sum_{l=0}^{\infty}w^l z^{-l}\]

So the output will be:

\[y_k(n)=w\sum_{l=0}^{\infty}w^l z^{-l}[x_j(n)]=\sum_{l=0}^{\infty}w^{l+1} x_j(n-l)\]

With a fixed $x_j(0)$, the output $y_k(n)$ will be:

• $\vert w \vert < 1$: converge
• $\vert w \vert = 1$: linearly diverge
• $\vert w \vert > 1$: expontially diverge

network architectures

• single-layer feedforward: one input, one layer of computing units (output layer), acyclic connections
• multilayer feedforward: one input layer, one (or more) hidden layers, and one output layer
• recurrent: feedback loop exists

Layers can be fully connected or partially connected.

design of a neural network

• select architecture, and gather input samples and train using a learning algorithm
• test with data not seen before
• it’s a data-driven, unlike conventional programming

similarity measures

• reciprocal of Euclidean distance $1/d(x_i,x_j)$:
  • $$d(x_i,x_j)=\vert \vert x_i -x_j \vert \vert = \left[ \sum_{k=1}^{m} (x_{ik}-x_{jk})^2\right]^{1/2}$$
• dot product
  • $$(x_i,x_j) = x_i^T x_j =\vert \vert x_i \vert \vert \centerdot \vert \vert x_j \vert \vert \cos \theta_{ij}$$

When $\vert \vert x_i \vert \vert = \vert \vert x_j \vert \vert = 1$:
\[d^2(x_i,x_j) = 2-2 x_i^T x_j\]

• mean vector $\mu_i = E[x_i]$
• Mahalanobis distance: $d_{ij}^2 = (x_i -\mu_i)^T \sum^{-1}(x_j- \mu_j)$
• Covariance matrix is assumed to be the same:
  • $$\sum=E[(x_i-\mu_i)(x_i-\mu_i)^T] = E[(x_j-\mu_j)(x_j-\mu_j)^T]$$